Синус и косинус в веб-дизайне

28.05.2024

Влад Мержевич

В CSS добавились новые стилевые тригонометрические функции, такие как sin(), cos(), tan() и др. В физике, математике и программировании, понятно, тригонометрические функции востребованы и нужны для различных вычислений. Но где их можно применять в веб-дизайне? В итоге появление всяких синусов и косинусов вызвало недоумение у многих веб-разработчиков. Давайте разбираться, где и как их можно использовать на практике.

Для начала вспомним, что собой вообще представляют синус и косинус на примере прямоугольного треугольника (рис. 1).

Рис. 1. Прямоугольный треугольник

Синусом угла φ называется отношение противолежащего катета к гипотенузе.

\sin φ = \frac{Противолежащий катет}{Гипотенуза} = \frac{B}{C}

Косинусом угла φ называется отношение прилежащего катета к гипотенузе.

\cos φ = \frac{Прилежащий катет}{Гипотенуза} = \frac{A}{C}

Синус и косинус используется при вычислении координат точки на окружности, когда нам известен радиус и угол φ между горизонтальной осью и линией, соединяющей нашу точку с центром окружности (рис. 2).

Рис. 2. Точка на окружности

Используя определения синуса и косинуса получаем формулы для вычисления координат точки x и y.

x = R·cos φ
y = R·sin φ

В веб-дизайне отсчёт координат начинается от левого верхнего угла элемента, а угол φ считается от вертикальной оси (рис. 3). При этом радиус окружности у нас привязан к размерам элемента и всегда равен 50%. Это же касается и центра окружности, она всегда располагается в центре элемента и её координаты тоже равны 50%.

Рис. 3. Координаты относительно элемента

С учётом этого, наши формулы для вычисления координат видоизменятся.

x = x₀ + R·sin φ = 50% + 50%·sin φ
y = y₀ − R·cos φ = 50% − 50%·cos φ

В качестве примера рассмотрим работу этих формул при создании многоугольников. Для этого будем использовать свойство clip-path и стилевую функцию polygon(), которой следут передать координаты вершин. Например, треугольнику требуется передать координаты x и y трёх точек, разделяя их запятыми.

clip-path: polygon(x1 y1, x2 y2, x3 y3);

Углы φ для треугольника легко получить, если разделить 360 на 3 и отмерить полученное значение от нуля. В итоге:

φ1 = 0; φ2 = 120°; φ3 = 240°;

В качестве значения функции sin() можно использовать градусы, радианы или повороты — sin(120deg) или sin(0.33turn). В итоге, для треугольника координаты вершин будут следующими:

clip-path: polygon(
  calc(50% + 50% * sin(0)) calc(50% - 50% * cos(0)),
  calc(50% + 50% * sin(0.33turn)) calc(50% - 50% * cos(0.33turn)),
  calc(50% + 50% * sin(0.66turn)) calc(50% - 50% * cos(0.66turn)),
);

В примере 1 с помощью указанного подхода показано создание пятиугольника, внутри которого располагается фоновое изображение.

Пример 1. Создание пятиугольника

<!DOCTYPE html>
<html lang="ru">
 <head>
  <meta charset="utf-8">
  <title>Синус и косинус</title>
  <style>
   .poly {
    --s: 200px; /* Размер элемента */
    width: var(--s); /* Ширина */
    height: var(--s); /* Высота */
    background: url(image/html-256.png) no-repeat 50% 50% / cover; /* Фон */
    clip-path: polygon(
      calc(50% + 50% * sin(0))       calc(50% - 50% * cos(0)),
      calc(50% + 50% * sin(0.2turn)) calc(50% - 50% * cos(0.2turn)),
      calc(50% + 50% * sin(0.4turn)) calc(50% - 50% * cos(0.4turn)),
      calc(50% + 50% * sin(0.6turn)) calc(50% - 50% * cos(0.6turn)),
      calc(50% + 50% * sin(0.8turn)) calc(50% - 50% * cos(0.8turn))
    );
   }
  </style>
 </head>
 <body>
  <div class="poly"></div>
 </body>
</html>

Результат данного примера показан на рис. 4.

Рис. 4. Пятиугольник

Конечно, использование в CSS формул, содержащих синусы и косинусы, кажется излишне сложным. Можно ведь просто предварительно вычислить требуемые координаты и подставить конкретные значения в функцию polygon(). Но приведённый метод имеет некоторые преимущества.

Размер элемента меняется в единственном месте (переменная --s), все остальные значения вычисляются браузером самостоятельно. Это позволяет легко менять размеры, задавая их в пикселях или процентах и подстраивая размер фигуры под размеры контейнера.
Использование формул в CSS позволяет создавать различные эффекты на основе переходов и анимации.

Рассмотрим ещё один пример, где три иконки располагаются на окружности в вершинах невидимого треугольника (рис. 5).

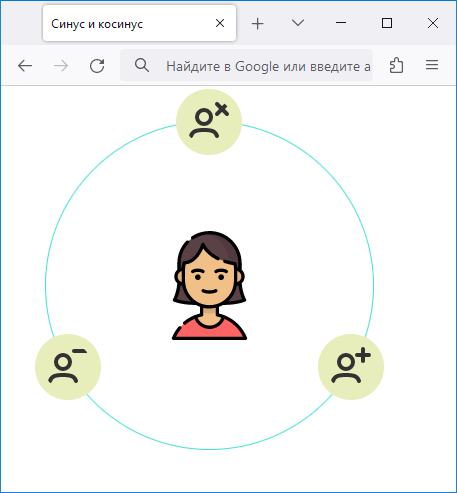
Рис. 5. Расположение иконок на окружности

Для позиционирования элементов будем использовать комбинацию свойств left и top. В качестве значений используем формулу для вершин треугольника.

left: calc(50% + 50% * sin(var(--angle)));
top: calc(50% - 50% * cos(var(--angle)));

Здесь для нашего удобства, вместо конкретных значений угла, применяется переменная --angle, которая определена для каждой иконки.

.user-icon-add   { --angle: 120deg; }

Поскольку свойства left и top отсчитываются от левого и верхнего краёв элемента, иконки надо будет сдвинуть влево и вверх на половину размера иконки. Функция translate() подходит для этого лучше всего.

transform: translate(-50%, -50%);

В примере 2 сделана простая анимация иконок при наведении на элемент. Сперва иконки располагаются в центре и невидимы, затем они «разбегаются» в разные стороны и встают на свои места.

Пример 2. Расположение иконок

<!DOCTYPE html>
<html lang="ru">
 <head>
  <meta charset="utf-8">
  <title>Синус и косинус</title>
  <style>
   .user {
    --W: 300px; /* Размер нашей области */
    --s_user: 100px; /* Размер картинки с пользователем */
    --s_icon: 60px; /* Размер иконок */
    width: var(--W); height: var(--W); /* Размеры элемента */
    border: 1px solid turquoise; /* Параметры рамки */
    border-radius: 50%; /* Радиус скругления */
    position: relative; /* Относительное позиционирование */
    margin: 2em; /* Добавляем пустое пространство вокруг */
   }
   .user-img {
    position: absolute; /* Абсолютное позиционирование */
    width: var(--s_user); height: var(--s_user); /* Размеры */
    left: calc(50% - var(--s_user) / 2); /* Располагаем по центру */
    top: calc(50% - var(--s_user) / 2); /* Располагаем по центру */
   }
   .user-icon {
    position: absolute; /* Абсолютное позиционирование */
    width: var(--s_icon); height: var(--s_icon); /* Размеры */
    left: 50%; top: 50%; /* Располагаем в центре */
    transform: translate(-50%, -50%); /* Сдвигаем на половину элемента */
    border-radius: 50%; /* Круглая иконка */
    padding: 0.5em; /* Расстояние от иконки до края */
    box-sizing: border-box; /* В размерах не учитываем padding */
    background-color: #e8edbc; /* Цвет фона */
    opacity: 0; /* Прозрачность */
    transition: 1s; /* Время перехода */
   }
   .user-icon:hover {
    background-color: tan; /* Цвет фона при наведении */
   }
   .user-icon-x     { --angle: 0deg;   }
   .user-icon-add   { --angle: 120deg; }
   .user-icon-minus { --angle: 240deg; }
   .user:hover .user-icon {
    left: calc(50% + 50% * sin(var(--angle)));
    top: calc(50% - 50% * cos(var(--angle)));
    opacity: 1; /* Иконка становится видимой */
   }
  </style>
 </head>
 <body>
  <div class="user">
   <div class="user-icons">
    <img src="image/user-x.svg" class="user-icon user-icon-x" alt="">
    <img src="image/user-add.svg" class="user-icon user-icon-add" alt="">
    <img src="image/user-minus.svg" class="user-icon user-icon-minus" alt="">
   </div>
   <img src="image/user-girl.svg" class="user-img" alt="">
  </div>
 </body>
</html>

Заключение

Да, CSS расширяет свои возможности и с каждым годом становится всё более сложным. Использование переменных и формул, содержащих математические операции и тригонометрические функции, перегружает стили и приближает CSS к языкам программирования, где без переменных и вычислений не обойтись. Всё это требует от веб-разработчика более глубоких знаний и высокой квалификации. Вместе с тем, новые стилевые функции увеличивают диапазон методов и техник, которые можно использовать в веб-дизайне. Те же тригонометрические функции, когда их распробуют и оценят, могут привести к моде на дизайн с круглым интерфейсом.

Синус и косинус в веб-дизайне

Заключение

Популярные материалы